Lec 25 - Inverse

Wednesday, March 07, 2012

9:29 AM

Recall:





 





 

Eg



 



 



 

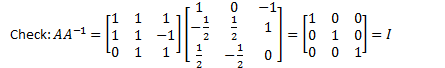
Eg











 







 



 





 



 

 

 

 Theorem: Invertible Matrix Theorem

 



 

1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 

 

 

 







 

 

Eg







 

 

 







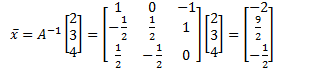
The row operations to get both RREF matrices are the same.



 

 Elementary Matrices

 

Definition



 

Eg







 

 Theorem

Every elementary matrix is invertible.

 

Proof:

For every elementary row operation, there is an inverse element row operation to undo it.



Q.E.D.

 

In fact, the inverse of any elementary matrix is the element matrix representing the inverse elementary row operation.

 

Eg







 

Eg





 

Eg





 

Eg